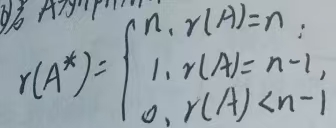k阶子式的定义
在矩阵A中任取k行k列(指数量而不是index),位于这些行列交叉处的k2个元素,不改变他们在A中的位置次序而得到的k阶行列式,称k阶子式
秩
矩阵A中有一个非零的r阶子式D,且所以的r+1阶子式(若存在)全等于0,那么D称为矩阵A的一个最高阶非零子式,r称为A的秩(非0子式的最高阶数)
当且仅当矩阵的秩等于行数和列数的最小值时,称为满秩阵(若为方阵则行列式不为0),反之为降秩阵
秩的性质
1.r(A)>=r 等价于 矩阵A中至少有一个r阶子式不等于0
2.r(A)<r 等价于 A中所有的r阶子式都为0
3.r(A) = r(AT)=r(-A)=r(kA) (其中k≠0)
4.r(A) = 0 等价于 A=O ,r(A) >=1 等价于A≠O
5.在A不是零矩阵的前提下,则A任意 两行(列)元素对应成比例 等价于 r(A) = 1
6.若A为行阶梯形矩阵,则A的秩即为其中非零行的数量
7.初等变换不改变矩阵的秩,若A~B则r(A) = r(B)
8.在A与B同型的前提下,A~B 等价于 r(A) = r(B)
9.若A的标准形为D,则A的秩即为D中1的个数
10.若A与B同型,则r(A±B)<=r(A)+r(B)
11.若A为m x n形矩阵,B为n x s形矩阵,则r(A)+r(B)-n <= r(AB) <= min(r(A),r(B))
12.若A为mxn形矩阵,B为nxs形矩阵,且AB = O,则r(A)+r(B)<=n
13.r(ATA)=r(AAT)=r(A)=r(AT)
14.若P、Q均可逆,则r(A)=r(PA)=r(AQ)=r(PAQ) (相当于做初等变换,不改变矩阵的秩) (用满秩阵去乘以一个矩阵时不改变这个矩阵的秩)
15.若A为n阶方阵(n>=2),A*为A的伴随矩阵,则有: