对于行数和列数大的矩阵,常常在A的行间作水平线,或列间做铅垂线把大矩阵分成小矩阵是分块法,每个小矩阵为A的子块,以子块为元素的矩阵称为分块矩阵。
运算规则
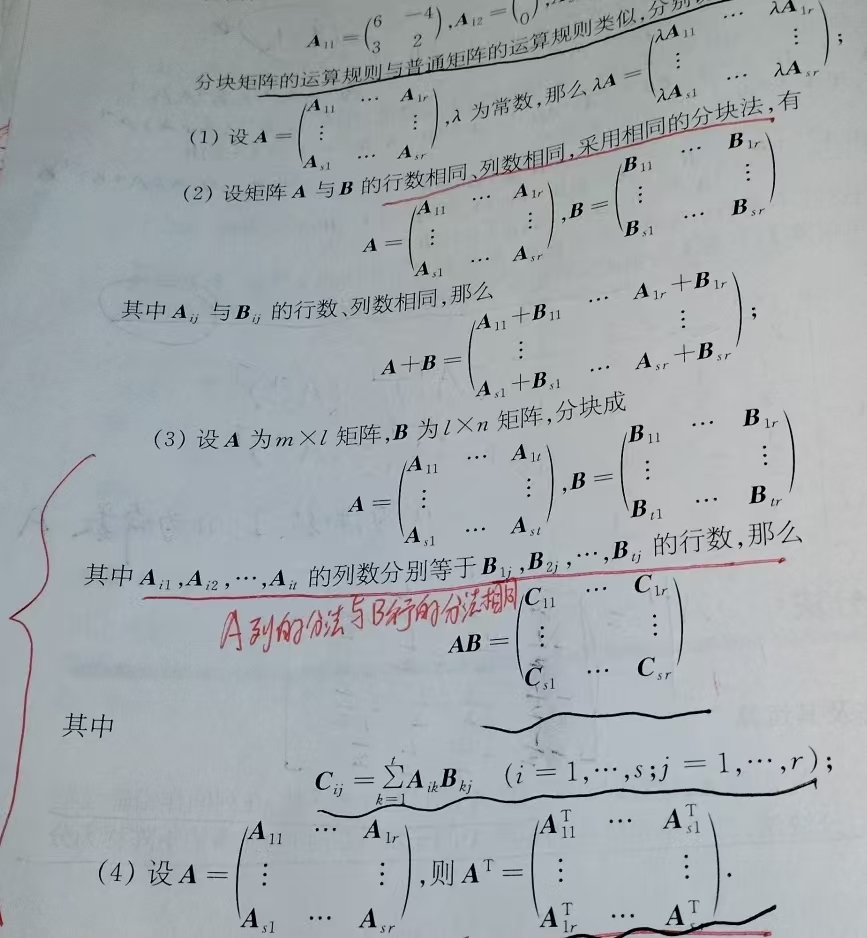
(1)和数乘相同
(2)一定要是相同形状的矩阵,并且要采取相同分块法
(3)A与B的形状符合乘法规则,并且A列的分法和B行的分法相同
(4)每个子块都要求转置,而且整体还要转置
常用分块形式及其应用
分块对角矩阵
除了主对角线上外全是零子块,主对角线上的子块都是方阵(阶数可以不相等)
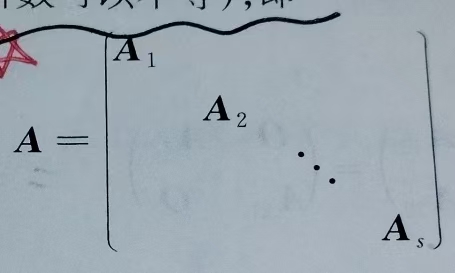
(1) 对于上述矩阵,有|A| = |A1||A2|…|As|
(2)如果上述子块都可逆,则有:主对角线上的子块直接取逆

ps:若是副对角线上的分块对角矩阵(虽然按照定义它不是的),取逆运算性质:副对角线上子块,取逆后再颠倒顺序

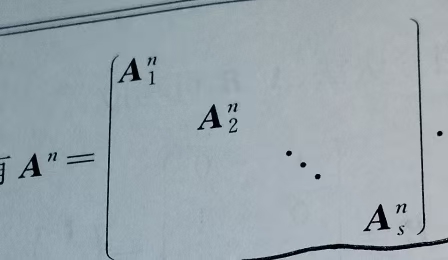
(3)分块矩阵的n次幂,即为主对角线子块取n次幂
正交矩阵
如果ATA = I ,则称A为正交矩阵
将m x n的矩阵A分块成 m x 1 或 1 x n ,则可以将每个子块看做A的一个向量
如果满足ATA = I ,则说明每个子块即为彼此垂直的单位向量,因此A为正交矩阵。