叠甲:自己当笔记用的,觉得乱的话别喷,有错的话请指正
1.通过定义计算
n阶行列式的值由多个项之和组成,取自所有的不同行不同列的n个元素,每个项的符号由以下规则确定
将元素的行标按自然顺序排列,列表的逆序数的奇偶性决定其正负(偶正奇负)
一般来说,二阶行列式直接计算,三阶行列式可用定义也可用其他办法化简
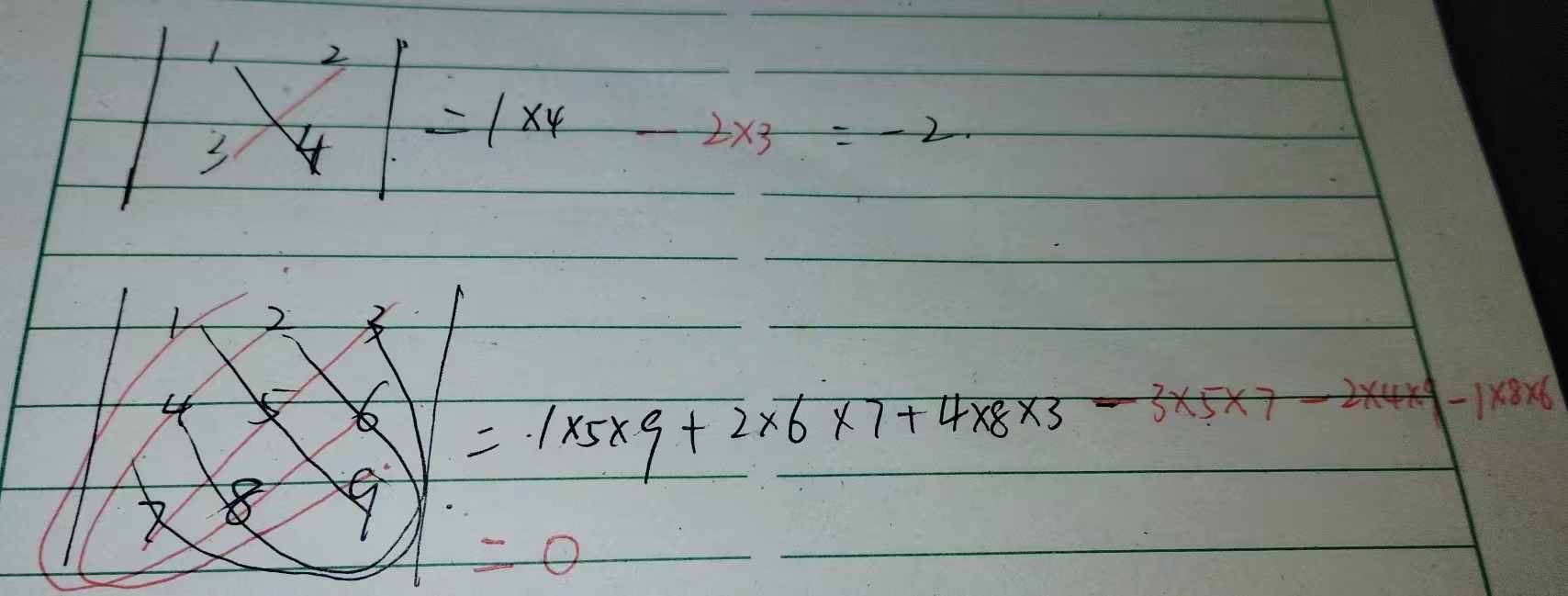
2.行列式按一行(列)展开
为了计算方便,一般选定0最多的行或列展开,大量元素可以通过乘0而消失
代数余子式
选定一个元素,将元素所在行和列的所有元素划去得到的新的行列式即为余子式
而将余子式乘上(-1)i+j (i和j是行列的标),即为代数余子式
求出代数余子式之后,将被展开行或列的元素乘以其代数余子式再相加,即可得到原行列式的值

3.行列式按多行(列)展开
用拉普拉斯定理(有点像按单行展开,总之都是找0多的元素,这里是找子行列式为0的个数多的方式展开)
用的最多的还是拉普拉斯定理的二级结论
4.通过行列式的初等变换来构造三角形行列式或者对角线行列式,从而简化计算
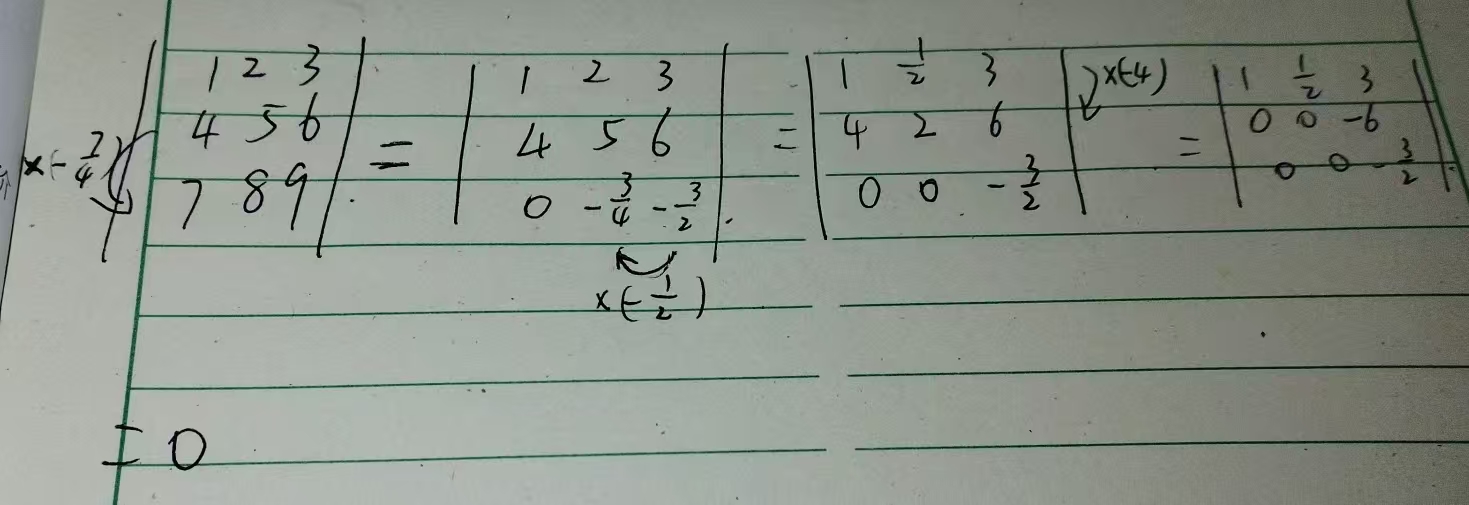
(未完工)