叠甲:自己当笔记用的,觉得乱的话别喷,有错的话请指正
1.方阵与其转置的行列式相等
2.行列式有两行(或列)相同,则行列式等于0 (推广:两行成比例则为0)
3.若某行元素是两组数的和,那么这个行列式就等于两个行列式的和,这两个行列式的其他部分和原来的行列式相同
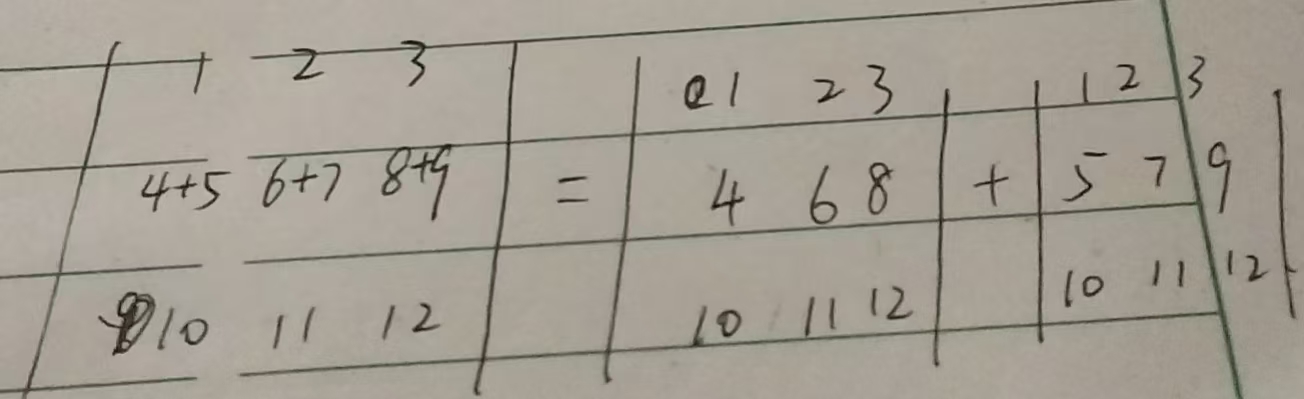
(等号两边对第i行展开,再使用乘法分配律即可证明)

4.若将初等行(列)变换用于n阶行列式,则有:
(1) 方阵A中某行(列)乘以a得到B,则|B|=a|A|(有几个公因子,就提几次)
(2) 方阵A中某行(列)的k倍加到另一行(列)得到B,则|B|=|A|
(3) 交换方阵A中任意两行(列)得到B,则|B|=-|A| (交换行列式两行要变号)
推论:
1.一行(列)元素全为0的行列式等于0
2.若有两行(列)元素对应成比例,则行列式等于0
3.对n阶方阵A,有|kA|=kn |A|
异乘变零定理
行列式某行所有元素与另一行中对应元素的代数余子项乘积的和等于0(列同理)
ai1Ak1+ai2Ak2+….+ainAkn = 0 (i≠k)
拉普拉斯定理
有点像按行(列)展开的推广
在n阶行列式D中,任取k行(列),由这行(列)组成的一切k阶子式N1,N2,…,与它们对应的代数余子式A1,A2…,乘积之和为D
D = N1A1+N2A2+…
二级结论
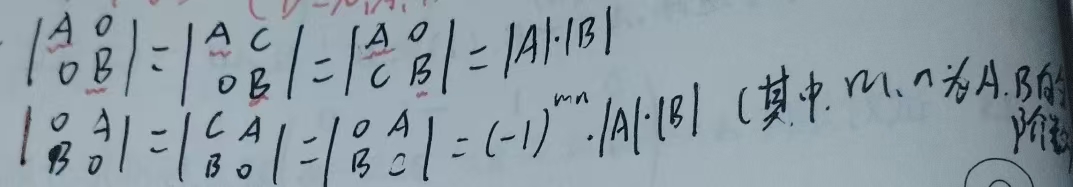
(主)对角线行列式,上下三角形行列式都是主对角线的元素之积
副对角线的行列式要在所有副对角线元素之积前加符号(-1)n(n-1)/2
奇数阶反对称矩阵的行列式必定为0,偶数阶未必
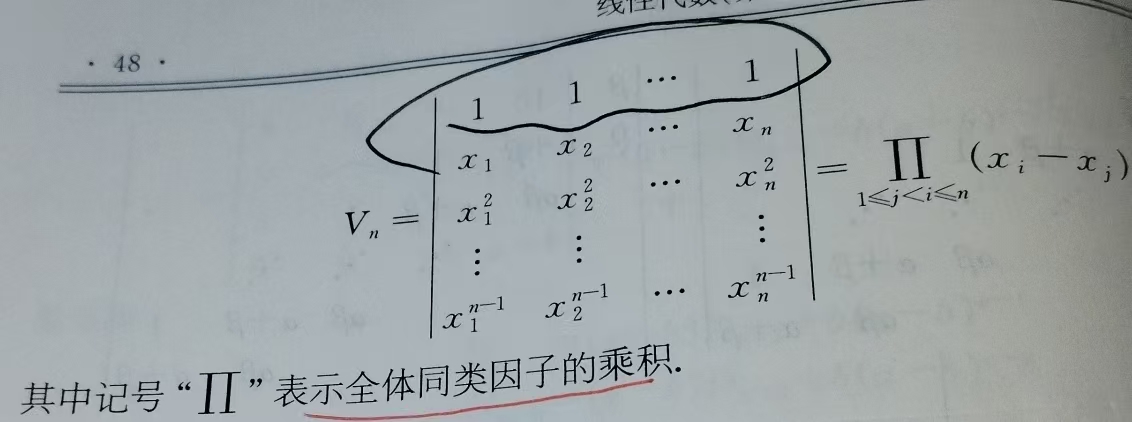
范德蒙德行列式