[PyTorch]使用神经网络处理线性回归问题

线性回归应该是神经网络所能处理的最简单的问题，通过此问题我们可以了解神经网络的基本流程。

1.准备训练数据集

生成一堆直线上取的散点，并且用随机数给它产生噪声

import random

path = r'D:\python\torch_study\datasets\liner.csv'

with open(path,'w') as f:
    for i in range(0,1000,1):
        x = i*0.1
        y = (random.random()-0.5)*0.1 + 2*x
        f.write('%f,%.4f\n' % (x,y))

2.分析并构建神经网络

因为我们是处理线性回归问题，而且每个元素都是标量，所以神经网络的隐藏层中仅需一个输入输出feature都为1的线型层。

class MyLinearNN(nn.Module):
    def __init__(self):
        super().__init__()
        if torch.cuda.is_available():
            self.linear = nn.Linear(1,1,True).cuda()
        else:
            self.linear = nn.Linear(1, 1, True)

    def forward(self,inp):
        return self.linear(inp)

3.选择损失函数和优化器

其实我也不知道怎么选…

因为没有聚类问题，所以损失函数选的MSELoss。

优化器选的最常见的随机梯度下降(SGD)

4.训练

训练范式:

计算模型输出(正向传播)->计算损失->清零梯度->反向传播损失->用优化器执行一次优化

out = myNN(x_tensor) # 计算当前模型的输出
loss = loss_fn(out,y_tensor) # 计算损失
# 优化前清零梯度
optimizer.zero_grad()
loss.backward() # 损失值反向传播
optimizer.step() # 执行一次优化

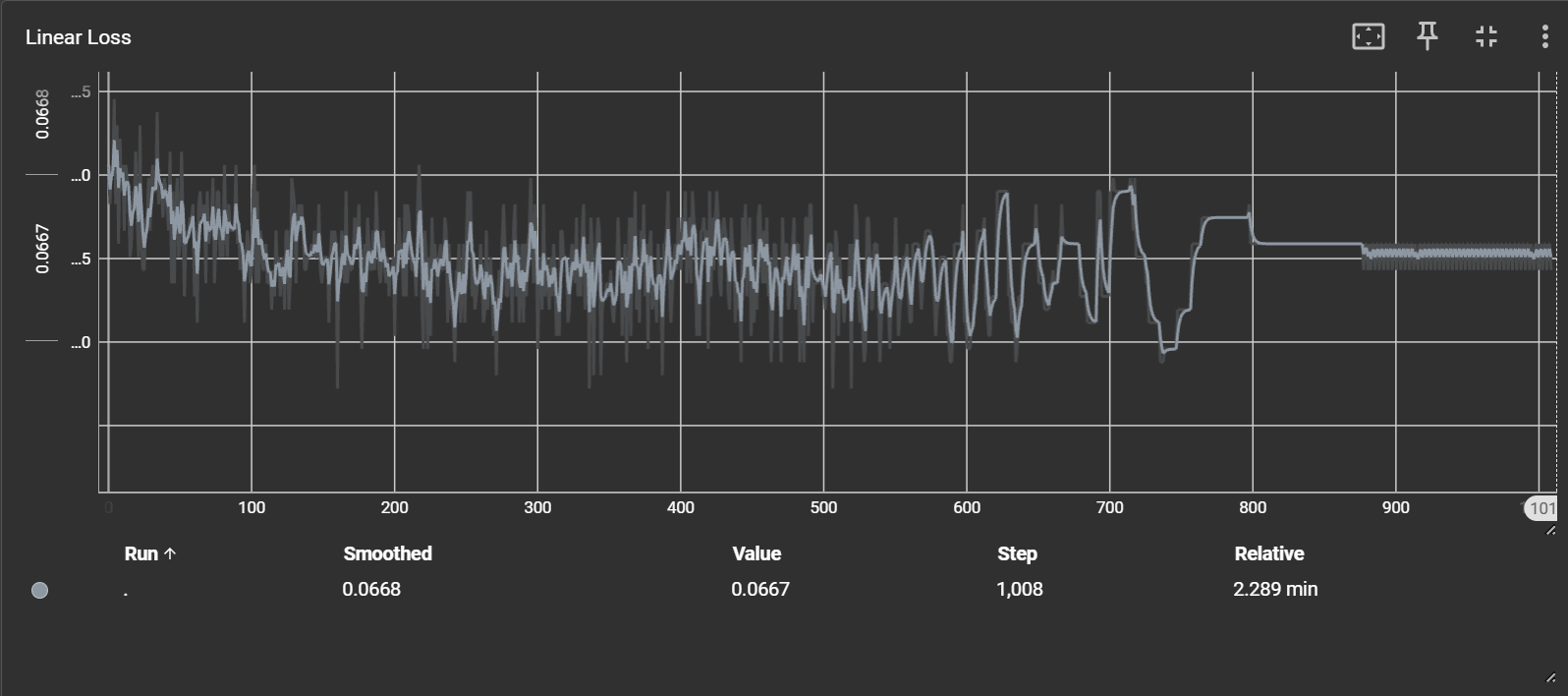
这是训练时损失函数的变化

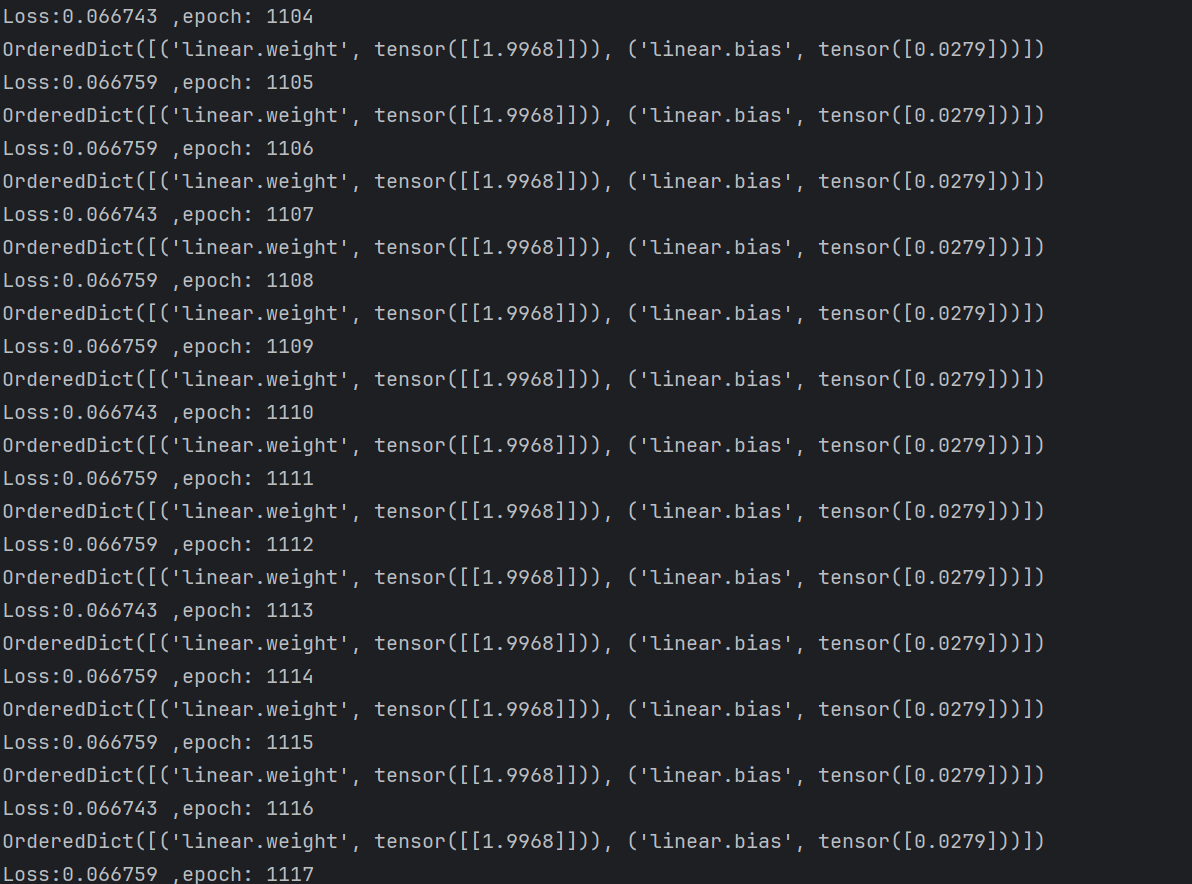
训练到一定程度模型参数几乎不变

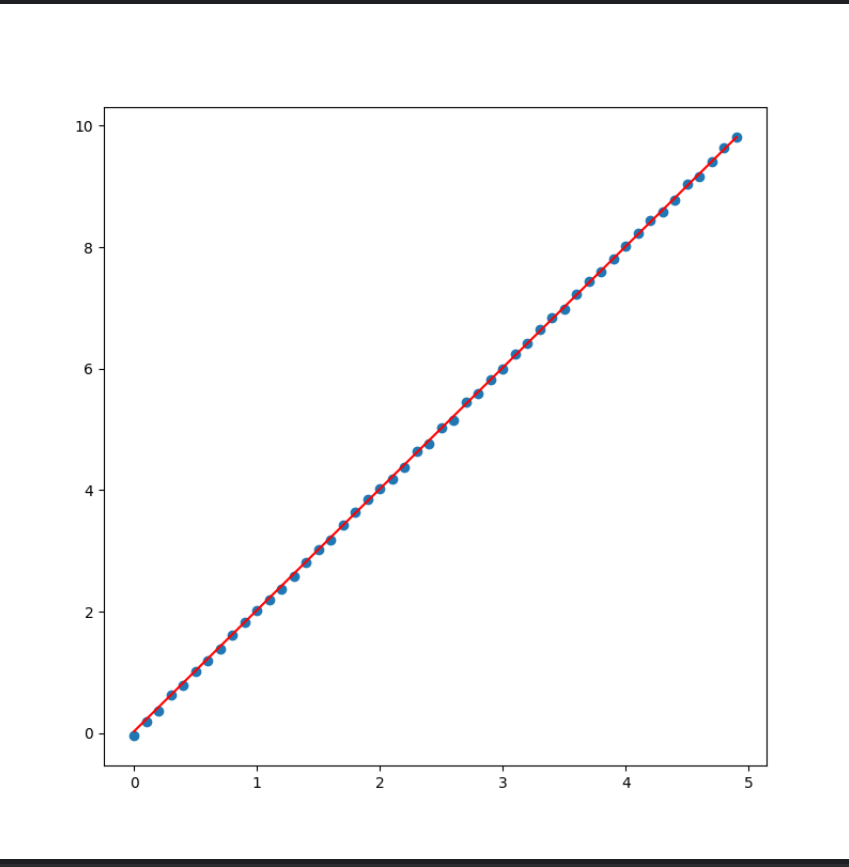
按照模型参数画出直线，并与数据点进行对比，发现比较吻合(只截取了0~5部分)

5.使用的源代码

https://github.com/MemoryController/linearmodel